Recentemente mi è stato chiesto di recuperare alcune password salvate all’interno di un modem Aethra versione 6.2.
La prima password che mi è stata proposta è u7qmn7yuyMM= chiaramente codificata in Base64, tuttavia però provando a convertirla ritorna dei valori non testuali.
Per risalire all’algoritmo utilizzato ho deciso di provare ad inserire varie password nel software per poi esportarle codificate e comparare i risultati con le versioni equivalenti in Base64.
Di seguito un breve estratto:
| In chiaro | Base64 + ??? | Base64 |
|---|---|---|
| K | uw== | Sw== |
| Q | wQ== | UQ== |
| U | xQ== | VQ== |
| U0 | xac= | VTA= |
| QQQ | wci1 | UVFR |
| QQR | wci2 | UVFS |
| AQR | sci2 | QVFS |
| QQQQ | wci1vA== | UVFRUQ== |
| QQQQQQQQ | wci1vLbKwcg= | UVFRUVFRUVE= |
| QQRQQQRQ | wci2vLbKwsg= | UVFSUVFRUlE= |
| AQR1AQR1 | sci2nKbKwqg= | QVFSMUFRUjE= |
| RRRRRRRR | wsm2vbfLwsk= | UlJSUlJSUlI= |
| SSSSSSSS | w8q3vrjMw8o= | U1NTU1NTU1M= |
| TTTTTTTT | xMu4v7nNxMs= | VFRUVFRUVFQ= |
| UUUUUUUU | xcy5wLrOxcw= | VVVVVVVVVVU= |
I risultati sono simili quando parliamo di una sola lettera, ma cambiano notevolmente quando proviamo ad aggiungere più lettere, come se la variazione non fosse costante.
Per riuscire a risolvere il problema avevo necessità di guardare da un secondo punto di vista, ho quindi provato a scendere di livello e convertire i caratteri in numeri seguendo la tabella ASCII.
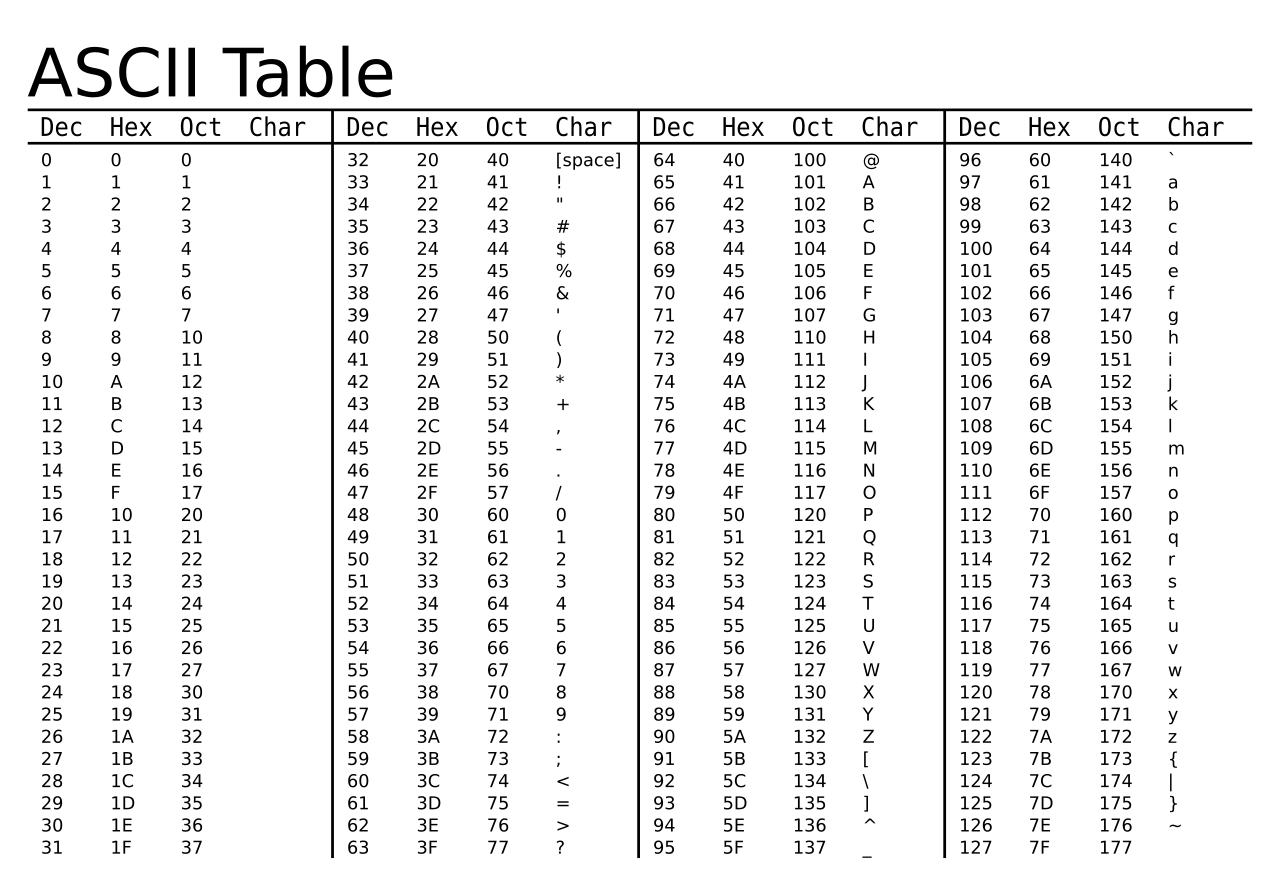
Ho quindi convertito tutti i valori in Base64 in caratteri, e successivamente nelle loro controparti numeriche:
| In chiaro | Base64 + ??? > ASCII | Base64 > ASCII |
|---|---|---|
| K | 187 | 75 |
| Q | 193 | 81 |
| U | 197 | 85 |
| U0 | 197 167 | 85 48 |
| QQQ | 193 200 181 | 81 81 81 |
| QQR | 193 200 182 | 81 81 82 |
| AQR | 177 200 182 | 65 81 82 |
| QQQQ | 193 200 181 188 | 81 81 81 81 |
| QQQQQQQQ | 193 200 181 188 182 202 193 200 | 81 81 81 81 81 81 81 81 |
| QQRQQQRQ | 193 200 182 188 182 202 194 200 | 81 81 82 81 81 81 82 81 |
| AQR1AQR1 | 177 200 182 156 166 202 194 168 | 65 81 82 49 65 81 82 49 |
| RRRRRRRR | 194 201 182 189 183 203 194 201 | 82 82 82 82 82 82 82 82 |
| SSSSSSSS | 195 202 183 190 184 204 195 202 | 83 83 83 83 83 83 83 83 |
| TTTTTTTT | 196 203 184 191 185 205 196 203 | 84 84 84 84 84 84 84 84 |
| UUUUUUUU | 197 204 185 192 186 206 197 204 | 85 85 85 85 85 85 85 85 |
Apparentemente ci sono buone notizie, in caso di valori ripetuti anche variando parzialmente il contenuto i valori uguali rimangono tali. Ciò può indicare che si tratta di un algoritmo lineare e non ricorsivo, il che semplifica molto la nostra ricerca.
Possiamo notare anche una cosa molto importante: valori uguali cambiano in base alla posizione ma rimangono costanti se altri valori all’interno della stringa variano.
Prendiamo la prima lettera di ogni stringa dalla colonna di centro e compariamola con la colonna di destra. La differenza tra i due valori è costante in tutte le stringhe: 112.
Prendiamo quindi l’ultima stringa dell’elenco UUUUUUUU e compariamo tutti i valori uno alla volta ottenendo la sequenza 112 119 100 107 101 121 112 119, la convertiamo in caratteri ed otteniamo pwdkeypw.
Avete riconosciuto l’algoritmo? Si tratta del cifrario di Vigenère, che utilizza un disco cifrante per codificare una sequenza di caratteri sfruttando una chiave che viene ripetuta, nel nostro caso pwdkey.
A questo punto abbiamo tutto il necessario per sviluppare l’algoritmo necessario a decifrare le nostre password:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#!/usr/bin/python
# -*- coding: UTF-8 -*-
import base64
# Coversione dei valori numerici in caratteri
def convert1(s):
new = ""
for x in s:
new += chr(x)
return new
# Coversione dei caratteri in valori numerici
def convert2(s):
new = []
for x in s:
if(type(x) == "String"):
new .append(ord(x))
else:
new .append(x)
return new
aencoded = input("Inserisci la password in base64: ")
adecoded = convert2(base64.b64decode(aencoded))
result = []
# Chiave: pwdkey
shifts = [112, 119, 116-16, 123-16, 117-16, 121]
# Left shift di tutti i valori secondo il cifrario di Vigenère
for i, val in enumerate(adecoded):
result.append(adecoded[i] - shifts[i%len(shifts)])
print("Risultato: " + convert1(result))
La domanda sorge quindi spontanea: era davvero necessario implementare questa cifratura per nascondere le password di un backup del modem? Algoritmi così semplici non garantiscono la sicurezza neanche utilizzando chiavi di cifratura complesse, pertanto con un po’ di pazienza e conoscenza si possono decifrare facilmente.